Time series analysis using ARIMA & LSTM - MODIS

Introduction

ARIMA (Autoregressive integrated moving average)

ARIMA can explain the time series pattern for given frequency or lag (hour, day and week …) and also predict furhter values.

ARIMA analysis will focus on the logic of model and how to select the three important terms of the model: p is the order of the AR term,

q is the order of the MA term, d is the number of differencing required to make the time series stationary. You can go to here for detailed explaination of ARIMA.

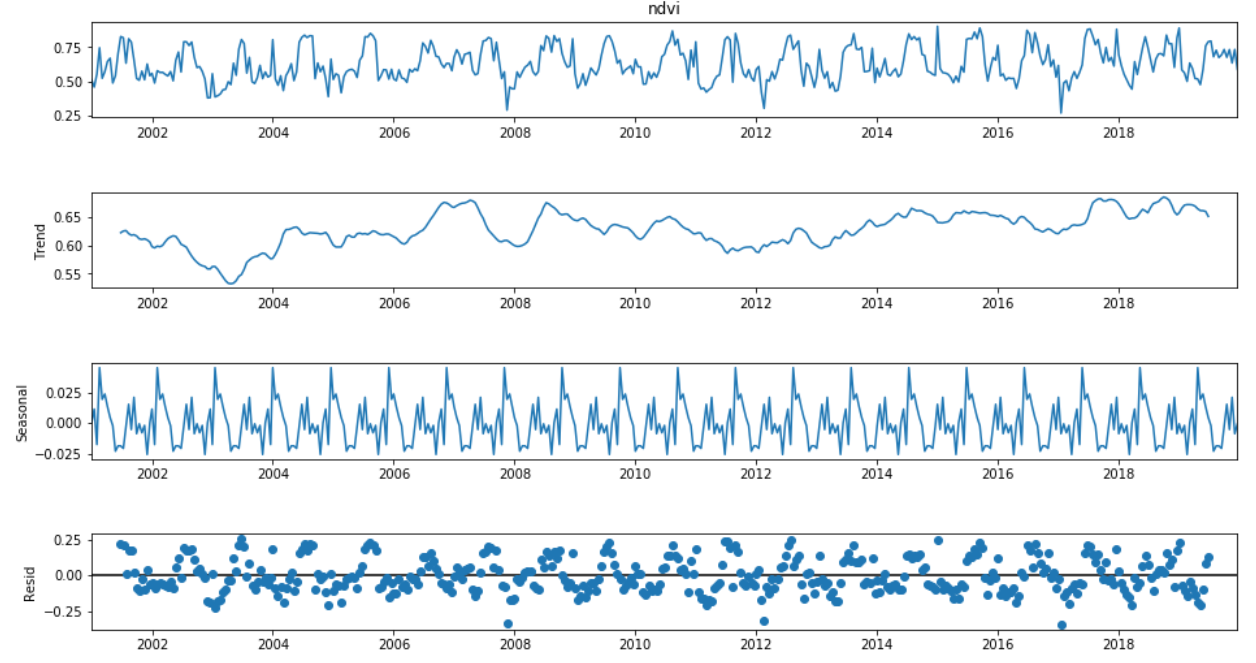
The first step of the model is to make the time series data stationary.

Stationarity

what is stationary?

1 The mean of the series should not be a function of time.

2 The variance of the series should not be a function of time. This property is known as homoscedasticity.

3 the covariance of the i th term and the (i + m) th term should not be a function of time

why the data need to be stationary?

Because, term ‘Auto Regressive’ in ARIMA means it is a linear regression model that uses its own lags as predictors.

When running a linear regression the assumption is that all of the observations are all independent of each other. In a time series, however, we know that observations are time dependent. It turns out that a lot of nice results that hold for independent random variables (law of large numbers and central limit theorem to name a couple) hold for stationary random variables. So by making the data stationary, we can actually apply regression techniques to this time dependent variable.

How to check Stationarity?

An augmented Dickey–Fuller test (ADF) tests the null hypothesis that a unit root is present in a time series sample. The alternative hypothesis is different depending on which version of the test is used, but is usually stationarity or trend-stationarity.

Basically, we are trying to whether to accept the Null Hypothesis H0 (that the time series has a unit root, indicating it is non-stationary) or reject H0 and go with the Alternative Hypothesis (that the time series has no unit root and is stationary).

We end up deciding this based on the p-value return.

    •A small p-value (typically ≤ 0.05) indicates strong evidence against the null hypothesis, so you reject the null hypothesis.

    •A large p-value (> 0.05) indicates weak evidence against the null hypothesis, so you fail to reject the null hypothesis.

Parameters of ARIMA

How to make data stationary and determine d?

The most common way is to difference it by substracting the previous values from the current values. This is also how to determine the d.

If d = 0, the input data of the model will be original data. If d = 1, it means we need to use the first difference of the time seriese.

Next, what are the ‘p’ and ‘q’ terms?

‘p’ is the order of the ‘Auto Regressive’ (AR) term. It refers to the number of lags of Y to be used as predictors. And ‘q’ is the order of the ‘Moving Average’ (MA) term. It refers to the number of lagged forecast errors that should go into the ARIMA Model.

How to determine p and q?

Identification of an AR model is often best done with inspecting the Partial Autocorrelation (PACF) plot.
- For an AR model, the theoretical PACF “shuts off” past the order of the model. The phrase “shuts off” means that in theory the partial autocorrelations are equal to 0 beyond that point. Put another way, the number of non-zero partial autocorrelations gives the order of the AR model. By the “order of the model” we mean the most extreme lag of x that is used as a predictor.
how to determine p: In particular, the partial autocorrelation at lag k is equal to the estimated AR(k) coefficient in an autoregressive model with k terms–i.e., a multiple regression model in which Y is regressed on LAG(Y,1), LAG(Y,2), etc., up to LAG(Y,k). Thus, by mere inspection of the PACF you can determine how many AR terms you need to use to explain the autocorrelation pattern in a time series: if the partial autocorrelation is significant at lag k and not significant at any higher order lags–i.e., if the PACF “cuts off” at lag k–then this suggests that you should try fitting an autoregressive model of order k
Identification of an MA model is often best done with the ACF rather than the PACF.
- For an MA model, the theoretical PACF does not shut off, but instead tapers toward 0 in some manner. A clearer pattern for an MA model is in the ACF. The ACF will have non-zero autocorrelations only at lags involved in the model.
how to determine q: to see first negative values of ACF plot’s corresponding x-axis (lag) value

Note: The sole reliance on the ACF and PACF to determine the p and q is NOT always correct. These plots just can help you understnad the ARIMA model and justify whether you can get a better model or worse one. Just try the simple model first and find a better model using AIC through multiple time exploration.

Project link: https://github.com/tankwin08/time_series_MODIS_ARIMA_LSTM